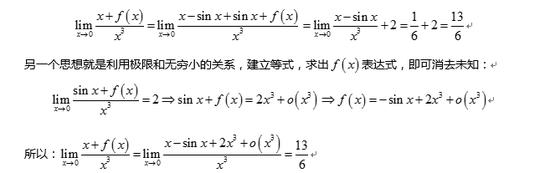2017年9月15日教育部考试中心发布了2018年全国硕士研究生入学统一考试数学考试大纲,与2017年大纲相比,整个考试大纲(数学一、数学二、数学三)包括标点符号在内,和去年的一模一样,所以同学们按照原来的计划复习即可,考试大纲没有任何的变化说明咱们考研命题的规律依然延续往年的原则,不会出现偏题、怪题、超纲题目,仍然以考查基本概念、基本理论和基本方法为主,所以大家放心复习,努力就一定会有更大的收获,更好的成绩。下面我就高等数学重要知识点—极限在考研中的命题规律,题型,例题等方面给大家进行总结,希望能给你带去更大的帮助。
极限的考查主要包含这几个角度:1。给定函数,求其极限;2。给定数列求极限;3。考查极限的应用;4。作为条件,解读信息。
1。函数极限:函数极限的求解,主要在于简化,拿到函数极限的问题,根据解题步骤:1)定型——判定未定式的类型,恒等变形为基本型来处理;2)简化——利用四则运算可以把存在的极限拆开,把非零的因式提取出来,整体因式的无穷小量进行等价替换;3)定法——若未定式是零比零形式,则考虑洛比达或者泰勒公式(出现了指数、三角函数、对数等优先利用泰勒相对简单)处理,若未定式是无穷比无穷,则考虑洛比达或者消去无穷大因式来解题。
2。数列极限:
n项无穷小的和,考虑定积分的定义;证明数列极限的存在性,优先考虑单调有界准则;求解未定式的数列极限,考虑连续化来求解;如果利用这些常规处理方法解决不了的问题,则利用夹逼准则进行计算。
3。会求函数极限,那么有关的应用:无穷小的比较、连续的问题、求间断点、渐近线、求某一点处的导数等问题,就迎刃而解,套相应的公式,计算极限即可。
4。如果题干当中给了极限作为条件,一般要从表达式中挖掘信息,下面就常考的几个形式给大家逐一讲解: