2014年的北京高考尘埃落定。纵观历年北京数学试卷,不难发现今年的高考试卷延续了近几年高考数学命题的风格——题干大气,内容丰富,题目难度适中,区分度较好。考试题目依然突出数学主干知识(函数与导数、数列、统计与概率、立体几何、解析几何等),整体比以往更偏重于对“三基”,即基础知识、基本技能和基本方法的考查。部分试题较往年有一定的创新性变化,考查了学生的数学能力。下面从几个方面对北京高考数学试卷进行分析。
总体分析
一. 试卷结构稳定
从试卷结构看,2014年北京高考试卷与往年一致:
| 北京高考数学试卷结构 | |||
| 题型 | 题目序号 | 分值 | |
| 第I卷 | 选择题 | 1~8 | 40 |
| 第II卷 | 填空题 | 9~14 | 30 |
| 解答题 | 15~20 | 80 | |
试卷结构这一点也符合2014年北京高考考试说明的要求。
二. 注重数学能力
2014北京卷体现了高考说明中对数学学科的要求:注重对通性通法的考查,注重对数学思维能力(空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力、分析问题和解决问题的能力)的考查。
北京高考数学试题总能使人感到清新自然,因为北京高考注重数学思维能力的考查。因此考生需要跳出“术数”的数学学习怪圈,不能用数学知识记忆、数学技巧来代替数学能力。正因为如此,北京市高考数学近几年连续涌现出很多“好题”,比如2010年解析几何大题、2011年第8题(整点个数范围)、2012年与2013年概率统计大题、同时还有近些年动态变化问题等等。例如2013年的解三角形大题,过程简单,思维能力要求却比较高,让人回味无穷。今年的考题在形式上很有创新,考生需要在考试中冷静处理分析。
三. 命题难度稳中有升
从整体难度看,2014北京市高考理科数学试题难度有一定上升,而文科数学难度略微下降。文科数学的难度变化主要体现在——以往压轴题考查学生对数学知识的综合应用能力,而今年却因为前面加入了一个数列解答题,使得以往的压轴题被常规的导数题;理科数学的难度变化是因为个别题目的命题方式推陈出新,使得学生解决问题时不太顺手导致的。客观而言,大多数题目难度与2013年基本持平。
| 近年北京高考数学平均分 | ||||||
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | |
| 理 | 102 | 92 | 101 | 95 | 101 | 97 |
| 文 | 90 | 92 | 93 | 88 | 88 | 101 |
2014北京卷试题延续了基础试题与中档试题占大多数的特点。虽然今年推陈出新,个别试题使部分同学临场发挥受影响,但这反过来说明平时的复习教学还有工作做的不到位,有墨守成规的倾向。这需要在今后的教学工作中做出相应的调整。
试题分析
试卷题目所对应知识点情况表:
| 题型 | 题号 | 主要考查知识(理) | 主要考查知识(文) | 分值 |
| 选
择 题 |
1 | 集合 | 集合 | 5 |
| 2 | 函数 | 函数 | 5 | |
| 3 | 参数方程 | 平面向量 | 5 | |
| 4 | 程序框图 | 程序框图 | 5 | |
| 5 | 数列 | 不等式 | 5 | |
| 6 | 线性规划 | 函数 | 5 | |
| 7 | 立体几何 | 圆 | 5 | |
| 8 | 实际应用 | 实际应用 | 5 | |
| 填
空 题 |
9 | 复数 | 复数 | 5 |
| 10 | 平面向量 | 圆锥曲线 | 5 | |
| 11 | 圆锥曲线 | 三视图 | 5 | |
| 12 | 数列 | 解三角形 | 5 | |
| 13 | 排列组合 | 线性规划 | 5 | |
| 14 | 三角函数 | 实际应用 | 5 | |
| 解
答 题 |
15 | 解三角形 | 数列 | 13 |
| 16 | 概率统计 | 三角函数 | 13 | |
| 17 | 立体几何 | 立体几何 | 14 | |
| 18 | 导数 | 概率统计 | 13 | |
| 19 | 圆锥曲线 | 圆锥曲线 | 14 | |
| 20 | 序列 | 导数 | 13 |
典型问题分析
理科


试题与分析

试题与分析

试题与分析

试题与分析
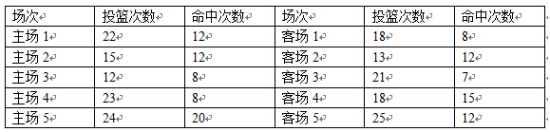
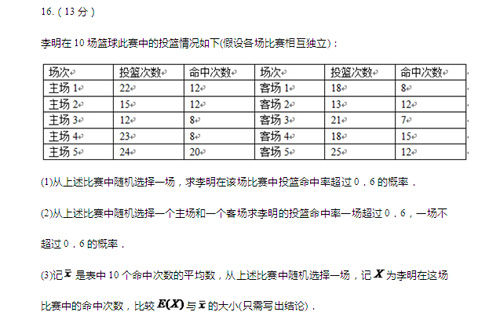
16.(13分)
李明在10场篮球此赛中的投篮情况如下(假设各场比赛相互独立):
图片
问题

答案

解析
一、试卷总体分析
2014年的重庆市数学高考是高中新课改后的第二次高考,试卷延续了近几年高考数学命题的风格,内容丰富,难易梯度明显,试卷整体难度适中,重在考查学生知识点的掌握、数学思维能力和数学知识的应用能力的培养,并体现了数学美感。
2014年数学试题总体上体现了“稳定和创新”,与2013年试题持平,试题无偏题怪,主干知识覆盖面较广。试题在题型设置、试卷结构、难度控制等方面都保持了稳定。试题难易梯度明显,由易到难便于学生稳定考试情绪、正常发挥水平;理科解答题的考试内容仍然是三角、概率、立体几何、导数、解析几何、数列与综合;文科解答题的考试内容是数列、概率、三角、导数、立体几何、解析几何;试题难易度把握很好,体现过度平稳性,和与教材联系紧密性。9题、10题、21、22题体现了很好的区分度,且21、22第一问入手容易,对后续问题的解决需要学生有较高的综合运用数学知识解决问题的能力,注重数学知识的融会贯通及数学能力的考查,很好的体现了能力立意,文科试题中应用性试题比例加重,试题背景贴合学生生活实际,理科试题很好地考查了学生后续的学习能力的考査,很好地体现了试题的选拔功能。试题充分体现了新课标精神,有利于重庆新课程改革的顺利开展。
总之,今年的数学试题平稳中有创新,科学性中有美感,理论性中有应用。既有利于中学数学的教学,又有利于高校的选拔,是一份很好的高考试卷。
二、各知识点分值分析
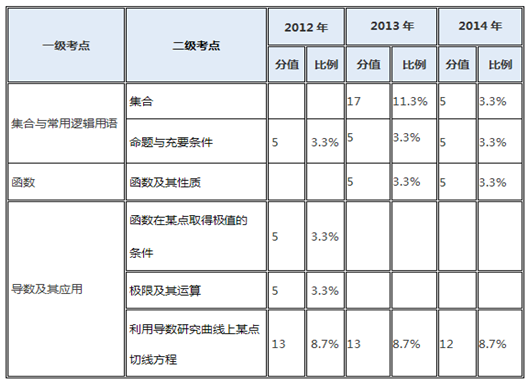
各知识点分值分析
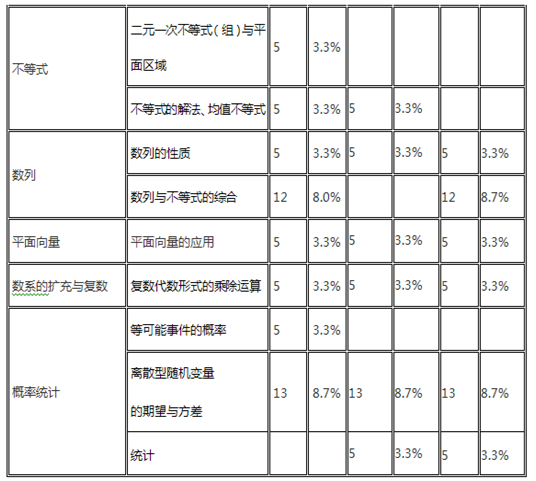
各知识点分值分析
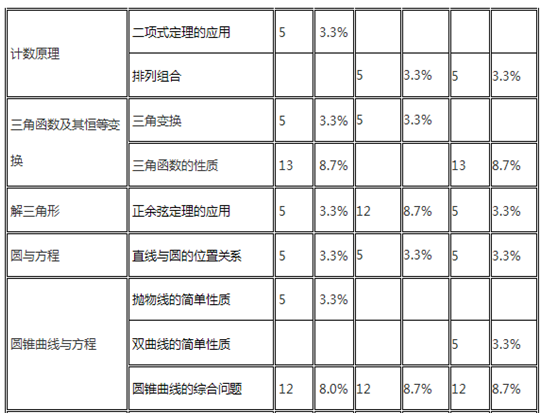
各知识点分值分析
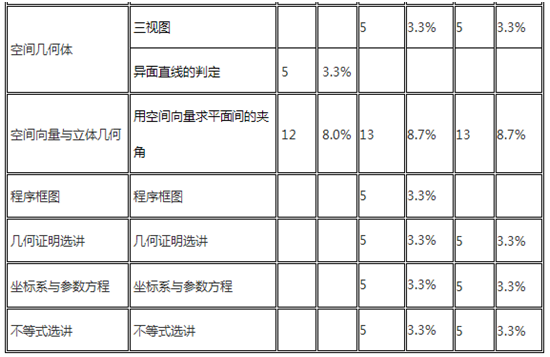
各知识点分值分析
三、典型试题分析
1。(5分)在复平面内表示复数i(1-2i)的点位于( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
正确答案:A
解析:i(1-2i)=i+2,所以表示复数i(1-2i)的点位于第一象限
2。(5分)对任意等比数列{an},下列说法一定正确的是( )
A、a1,a3,a9成等比数列
B、a2,a3,a6成等比数列
C、a2,a4,a8成等比数列
D、a3,a6,a9成等比数列
正确答案:D
解析:用等比中项公式,本题考查了等比数列的判定性质:从等比数列里每隔相同项抽取一个数形成的新数列也是等比例数列,所以很容易就可以得出选项D是正确的。

问题与答案

解析
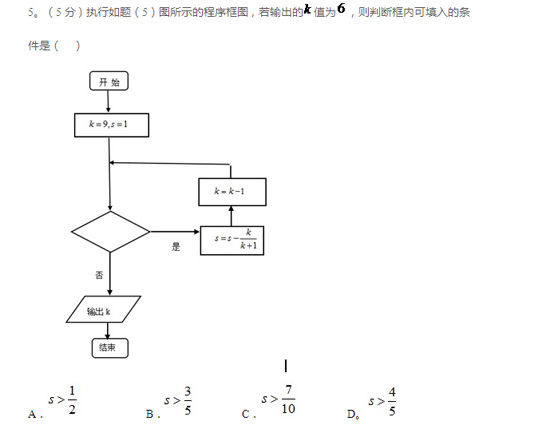
问题

答案

问题与答案
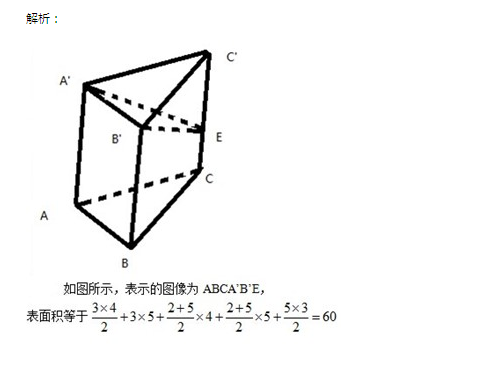
解析

问题与解析

问题与答案

解析

问题与答案

解析

问题与答案

问题

解析

解析

问题

解析

解析

解析

问题与解析

解析

问题

解析

点评
四、备考建议
(一)要培养良好的解题习惯,做到“会做=拿满分”
有不少学生在平时的学习中,题目读完后,发现类型、方法都与做过的某某题类似,就轻易跳过不去管了,殊不知,“会而不对、对而不全”是一名普通学生和一名优秀学生的重要区别。因此在复习中,做题一定要彻底:推理过程严密、显示主要步骤,考虑问题全面,正确书写解题过程和答案,切不可走马观花,凭想当然去处理遇到的题目。
1.会而不对:做题时不是束手无策,而是在正确的思路上,或考虑不周、或推理不严、或书写不准,最后答案是错的,这叫“会而不对”。
2.对而不全:做题思路大体正确,最终结论也出来了,但丢三落四,或缺欠重大步骤,中间某一逻辑点过不去;或遗漏某一特殊情况、讨论不够完备;或潜在假设、或以偏概全,这叫“对而不全”。
针对以上两种情况,必须在平时的训练中做“综合治理”:会做的题目,要特别注意表达的准确、考虑的周密,书写的规范、语言的科学,做到“会而对、对而全、全而优”。
切记:“不对=不会”。
(二)提高解三角题、数列题、立体几何题、概率统计题的准确率
进入高三后,每个学生对自己的知识能力水平,应该有个大致的定位,也就是一份高考水平的数学试卷,你打算做多少题,哪些题是必须拿分的,哪些题是可以放弃的。所谓“舍得”,有所舍弃才能有所得。三角函数、数列、立体几何、概率统计题的高考定位是“中低档难度”,对大部分学生来说,在复习时,一定要把这些部分的题目做透。抓好这些题的满分率是提高总分的有效途径。其中:
1.三角函数:关键是抓三角函数的图象特征,掌握简单的三角恒等变换、正弦定理和余弦定理;关注测量及三角应用题。
2.数列:关键是抓等差数列和等比数列的定义和“基本量法”,关注数列应用题。
3.立体几何:关键是抓垂直与平行。垂直是解立体几何题的一个关键突破口。会建立空间直角坐标系,用空间向量的方法解决空间中的角度问题,并能正确计算。
4.概率统计:关键是重视概率思想与统计思想,重视统计量及统计中数据处理的方法,注意古典概型和几何概型概率计算。重视排列组合在求概率中的应用,掌握几种特殊的分布(几何分布、二项分布等)。理解数学期望和方差的实际含义和计算公式。
(三)对一些“小题”要有足够的重视
所谓的“小题”一般指那些只在选择题或填空题中出现、不易同高中数学其他知识点综合考查的题目,比如线性回归问题、程序框图问题、正态分布问题、极坐标、参数方程、几何证明等,这些题目一般比较简单,只要把基本的知识掌握了,处理起来还是比较容易的。不要忘了,高考中在哪部分知识上得分是没有差别的,因此在第一轮复习中,千万不能歧视或忽略这些“不重要”的“小题”所对应的知识点。

