
提到中考数学,就不得不提二次函数。对于二次函数,相信大家并不陌生,特别是进入初三之后,很多关于压轴题的讲解,都是围绕二次函数展开,如二次函数综合问题、二次函数动点问题、二次函数分类讨论、二次函数与几何等综合问题,这些题型都是全国各地中考数学非常喜欢考查的对象,大部分时候都是作为压轴题来考查考生。
中考既考查二次函数及其图象的有关基础知识,同时以二次函数为背景的应用性问题也是命题热点之一。与二次函数有关的实际应用题,近年在各地中考数学中频频出现,因此,无论是二次函数的新课学习还是中考复习,大家都要及时关注这一热点。
典型例题分析1:
一玩具厂去年生产某种玩具,成本为10元/件,出厂价为12元/件,年销售量为2万件。今年计划通过适当增加成本来提高产品档次,以拓展市场。若今年这种玩具每件的成本比去年成本增加0.7X倍,今年这种玩具每件的出厂价比去年出厂价相应提高0.5X倍,则预计今年年销售量将比去年年销售量增加X倍(本题中0<X≤11)。
(1)用含X的代数式表示,今年生产的这种玩具每件的成本为 元,今年生产的这种玩具每件的出厂价为 元。
(2)求今年这种玩具的每件利润Y元与X之间的函数关系式。
(3)设今年这种玩具的年销售利润为W万元,求当X为何值时,今年的年销售利润最大?最大年销售利润是多少万元?
注:年销售利润=(每件玩具的出厂价﹣每件玩具的成本)×年销售量。
解(1)10+7x;12+6x;
(2)y=(12+6x)﹣(10+7x),
∴y=2﹣x (0<x<2);
(3)∵W=2(1+x)y
=﹣2(1+x)(x﹣2)
=﹣2x2+2x+4,
∴W=﹣2(x﹣0.5)2+4.5
∵﹣2<0,0<x≤11,
∴W有最大值,
∴当x=0.5时,W最大=4.5(万元)。
答:当x为0.5时,今年的年销售利润最大,最大年销售利润是4.5万元。
考点分析:
二次函数的应用;应用题。
题干分析:
(1)根据题意今年这种玩具每件的成本比去年成本增加0.7x倍,即为(10+100.7x)元/件;这种玩具每件的出厂价比去年出厂价相应提高0.5x倍,即为(12+120.5x)元/件;
(2)今年这种玩具的每件利润Y等于每件的出厂价减去每件的成本价,即y=(12+6x)﹣(10+7x),然后整理即可;
(3)今年的年销售量为(2+2x)万件,再根据年销售利润=(每件玩具的出厂价﹣每件玩具的成本)×年销售量,得到W=﹣2(1+x)(x﹣2),然后把它配成顶点式,利用二次函数的最值问题即可得到答案。
解题反思:
本题考查了二次函数的顶点式:y=a(x﹣k)2+h,(a≠0),当a<0,抛物线的开口向下,函数有最大值,当x=k,函数的最大值为h。也考查了代数式的表示和利润的含义以及配方法。
函数问题一直是初中数学的核心内容,而二次函数的应用更是中考命题的热点之一,其题型变化一直受到命题老师的高度关注。纵观近几年全国各地中考数学试题为例,认真分析题型当中设置的常见手法和技巧,对大家正确掌握应对方法,破除解题障碍有着积极的意义。
典型例题分析2:
一玩具厂去年生产某种玩具,成本为10元/件,出厂价为12元/件,年销售量为2万件。今年计划通过适当增加成本来提高产品档次,以拓展市场。若今年这种玩具每件的成本比去年成本增加0.7x倍,今年这种玩具每件的出厂价比去年出厂价相应提高0.5x倍,则预计今年年销售量将比去年年销售量增加x倍(本题中0<x≤11)。
(1)用含x的代数式表示,今年生产的这种玩具每件的成本为 元,今年生产的这种玩具每件的出厂价为 元。
(2)求今年这种玩具的每件利润y元与x之间的函数关系式。
(3)设今年这种玩具的年销售利润为w万元,求当x为何值时,今年的年销售利润最大?最大年销售利润是多少万元?
注:年销售利润=(每件玩具的出厂价-每件玩具的成本)×年销售量。
解(1)10+7x;12+6x;
(2)y=(12+6x)-(10+7x),∴y=2-x (0<x<2);
(3)∵w=2(1+x)y=-2(1+x)(x-2)=-2x2+2x+4,
∴w=-2(x-0.5)2+4.5
∵-2<0,0<x≤11,
∴w有最大值,
∴当x=0.5时,w最大=4.5(万元)。
答:当x为0.5时,今年的年销售利润最大,最大年销售利润是4.5万元。
考点分析:
二次函数的应用;应用题。
题干分析:
(1)根据题意今年这种玩具每件的成本比去年成本增加0.7x倍,即为(10+100.7x)元/件;这种玩具每件的出厂价比去年出厂价相应提高0.5x倍,即为(12+120.5x)元/件;
(2)今年这种玩具的每件利润y等于每件的出厂价减去每件的成本价,即y=(12+6x)-(10+7x),然后整理即可;
(3)今年的年销售量为(2+2x)万件,再根据年销售利润=(每件玩具的出厂价-每件玩具的成本)×年销售量,得到w=-2(1+x)(x-2),然后把它配成顶点式,利用二次函数的最值问题即可得到答案。
解题反思:
本题考查了二次函数的顶点式:y=a(x-k)2+h,(a≠0),当a<0,抛物线的开口向下,函数有最大值,当x=k,函数的最大值为h。也考查了代数式的表示和利润的含义以及配方法。

很多考生在复习过程中,对应用题的关注度并不高,但其实它一直是中考数学必考的解答题。在历年的中考数学中,二次函数都是考试的必考知识内容,而二次函数的应用题是重点中的重点,相当一部分考生在中考数学当中失分比较严重。
通过例题的讲解分析,我们要学会在应用题上找到解题的关键点,并通过习题训练,及时掌握一定的中考二次函数应用题解题技巧。
典型例题分析3:
课本中有一个例题:
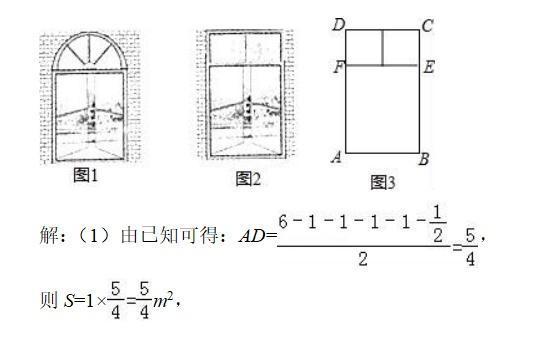
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2。
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明。

考点分析:
二次函数的应用。
题干分析:
(1)根据矩形和正方形的周长进行解答即可;
(2)设AB为xcm,利用二次函数的最值解答即可。
典型例题分析4:
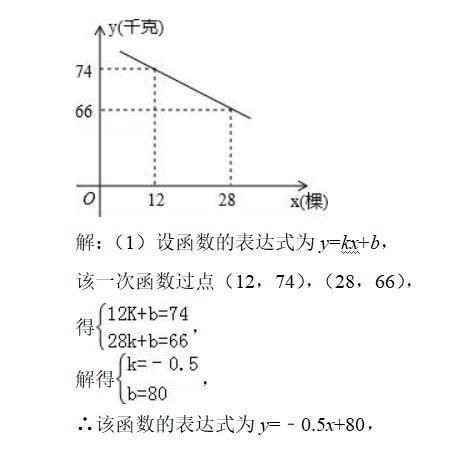
某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低。若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示。
(1)求y与x之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?

考点分析:
二次函数的应用。
题干分析:
(1)函数的表达式为y=kx+b,把点(12,74),(28,66)代入解方程组即可。
(2)列出方程解方程组,再根据实际意义确定x的值。
(3)构建二次函数,利用二次函数性质解决问题。
应用二次函数知识去解决的实际问题,我们称这类问题为二次函数应用题,大家一定要认识到二次函数应用题一直是中考数学的命题热点,其中一些命题设计新颖,创意别具一格,在复习过程中一定要抓住命题特点及解题思路。
来源:吴国平数学教育
责任编辑:陈熙


